MATLAB提供命令与转换，如拉普拉斯及傅立叶变换。变换被用来作为一种工具，用于简化数据从另一个角度分析在科学和工程。
例如，傅立叶变换，使我们能够表示为时间的函数的频率的函数的信号转换。拉普拉斯变换，使我们能够转换成差分方程的代数方程。
MATLAB提供的拉普拉斯，傅立叶和FFT命令拉普拉斯，傅立叶和快速傅立叶变换工作。
时间函数f（t）的拉普拉斯变换的函数，由下式给出下面的积分：
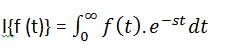
拉普拉斯变换的变换函数f（t）也表示为F（次）。可以看到这种变换或一体化进程的符号变量t的函数，F（T），转换成另一个函数F（s）和另一个变量s。
拉普拉斯变换将微分方程转化为代数。要计算一个函数f（t）的拉普拉斯变换，这样写：
laplace(f(t))示例
在这个例子中，我们会计算一些常用函数的拉普拉斯变换。
创建一个脚本文件，并键入下面的代码：
syms s t a b w laplace(a) laplace(t^2) laplace(t^9) laplace(exp(-b*t)) laplace(sin(w*t)) laplace(cos(w*t))当运行该文件，它会显示以下结果：
ans = 1/s^2 ans = 2/s^3 ans = 362880/s^10 ans = 1/(b + s) ans = w/(s^2 + w^2) ans = s/(s^2 + w^2)
MATLAB允许我们计算拉普拉斯逆变换使用命令ilaplace。
例如
ilaplace(1/s^3)
MATLAB将执行上面的语句，并显示结果：
ans = t^2/2
创建一个脚本文件，并键入下面的代码：
syms s t a b w ilaplace(1/s^7) ilaplace(2/(w+s)) ilaplace(s/(s^2+4)) ilaplace(exp(-b*t)) ilaplace(w/(s^2 + w^2)) ilaplace(s/(s^2 + w^2))当运行该文件，它会显示以下结果：
ans = t^6/720 ans = 2*exp(-t*w) ans = cos(2*t) ans = ilaplace(exp(-b*t), t, x) ans = sin(t*w) ans = cos(t*w)
傅立叶变换，常用的时间变换的数学函数，函数f（t），进入一个新的功能，有时记为或F组，其参数是频率与周期/秒（赫兹）或每秒弧度的单位。新的函数，然后被称为傅里叶变换和/或函数f的频谱。
创建一个脚本文件，并键入下面的代码：
syms x f = exp(-2*x^2); %our function ezplot(f,[-2,2]) % plot of our function FT = fourier(f) % Fourier transform当您运行该文件，MATLAB会绘制图，并显示以下结果
FT = (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2折线图的傅里叶变换为：
ezplot(FT)傅立叶逆变换
MATLAB提供的 ifourier 命令，用于计算一个函数的傅立叶逆变换。例如
MATLAB将执行上面的语句，并显示结果：
f = -2/(pi*(x^2 + 1))
