单关键字和多关键字

文件中任一记录R[i]的关键字均由d个分量

构成。

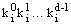
若这d个分量中每个分量都是一个独立的关键字，则文件是多关键字的(如扑克牌有两个关键字：点数和花色)；否则文件是单关键字的，

(0≤j<d)只不过是关键字中其中的一位(如字符串、十进制整数等)。

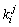
多关键字中的每个关键字的取值范围一般不同。如扑克牌的花色取值只有 4 种，而点数则有 13 种。单关键字中的每位一般取值范围相同。

基数

设单关键字的每个分量的取值范围均是：

C0≤kj≤Crd-1(0≤j<d)

可能的取值个数 rd 称为基数。

基数的选择和关键字的分解因关键宇的类型而异:

(1) 若关键字是十进制整数，则按个、十等位进行分解，基数 rd=10，C0=0，C9=9，d 为最长整数的位数； (2) 若关键字是小写的英文字符串，则 rd=26，Co='a'，C25='z'，d 为字符串的最大长度。

基数排序的基本思想

基数排序的基本思想是：从低位到高位依次对 Kj(j=d-1，d-2，…，0)进行箱排序。在 d 趟箱排序中，所需的箱子数就是基数 rd，这就是"基数排序"名称的由来。

基数排序的排序过程

要排序的记录关键字取值范围是 0 到 99 之间的整数(36，5，16，98，95，47， 32，36，48)。对这些关键字进行基数排序的过程。

基数排序的类型说明和算法描述

要保证基数排序是正确的，就必须保证除第一趟外各趟箱排序是稳定的。

算法分析

若排序文件不是以数组 R 形式给出，而是以单链表形式给出(此时称为链式的基数排序)，则可通过修改出队和人队函数使表示箱子的链队列无须分配结点空间，而使用原链表的结点空间。人队出队操作亦无需移动记录而仅需修改指针。虽然这样一来节省了一定的时间和空间，但算法要复杂得多，且时空复杂度就其数量级而言并未得到改观。

基数排序的时间是线性的(即 O(n))。

基数排序所需的辅助存储空间为 O(n+rd)。

基数排序是稳定的。